Euclides de Alexandria e a mesa bamba

Você já se sentou para tomar alguma bebida (ou mesmo uma sopa) e quando encostou seus cotovelos na mesa ela se moveu e o líquido caiu do recipiente? Se sim, muito provavelmente a mesa tinha quatro pernas. Se tivesse três, a chance de isso ocorrer diminuiria, e muito! Vamos ver por quê.

Assumiremos que o chão é regular ou minimamente ondulado, de forma que ele não contribua para a instabilidade da mesa. Ou seja, o chão é um plano na geometria clássica, ou Euclidiana. E que o problema está, como na maioria das vezes, de fato, na irregularidade do comprimento ou da posição das pernas, impedindo o apoio concomitante dos quatro pés.

Definição de plano na geometria

Um plano, da forma como é tratado pela geometria, pode ser definido como um conjunto infinito de pontos formando uma superfície plana que se estende em todas as direções, infinitamente. Assim, um plano tem comprimento e largura (infinitos), mas não tem altura.

Há um postulado que diz: “três pontos não colineares (fora da mesma linha) determinam um e somente um plano”. Euclides de Alexandria deve ter ensinado isso a seus discípulos, há mais ou menos 2300 anos, embora não encontremos essa formulação em seus livros, nem mesmo entre os postulados de sua obra mais famosa, “Os elementos” (escrito por volta do ano 300 a.C.). Não é estranho imaginarmos que essa noção vigorasse à época, mesmo que em outras palavras.

Outra forma de definirmos plano – através de mais um postulado – é: “um plano contém ao menos três pontos não colineares”. Na verdade, um plano tem inúmeros ou infinitos pontos, desde que ao menos um seja não colinear. Os dois modos são complementares ao enunciar esse conhecimento. A figura abaixo mostra três pontos não colineares no mesmo plano, que chamei de “beta”.

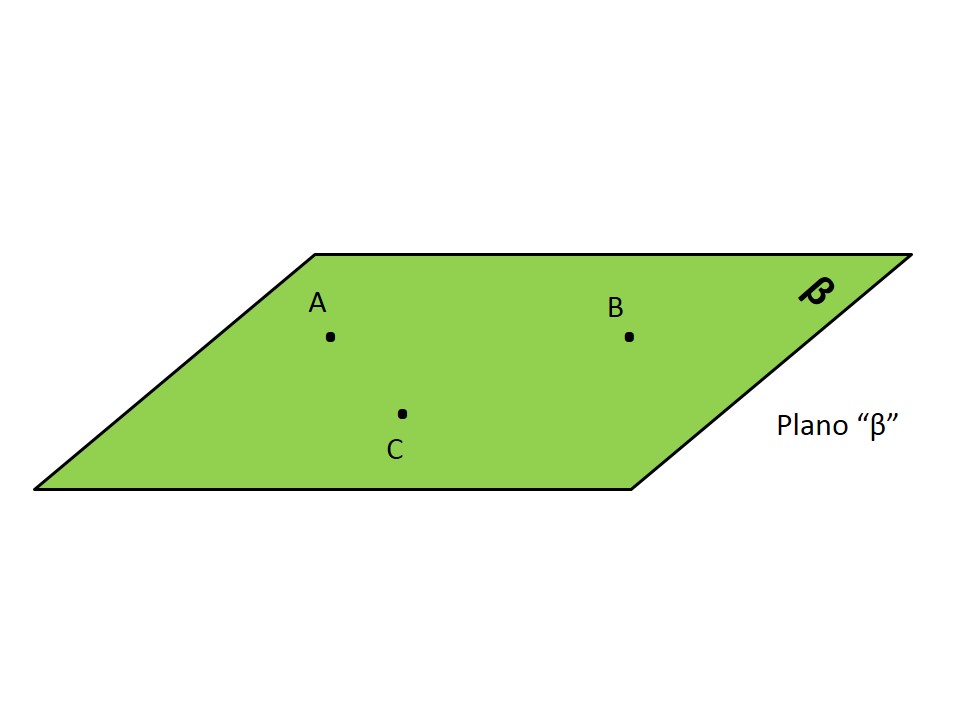
Postulados

E o que é um postulado? Postulado é uma afirmação (quase sempre uma informação ou conhecimento) aceita como verdadeira sem necessidade de prova. No livro “Os elementos”, há cinco postulados. O primeiro deles será útil para o que tratamos nesse texto e diz: “fique postulado traçar uma reta de todo ponto até todo ponto”*. Isto é fácil de entender porque intuitivo. Olhe a figura abaixo, na qual os pontos A e B pertencem à mesma reta (colineares), mas não o ponto C. A exposição gráfica auxilia bastante o entendimento. Na época de Euclides, problemas matemáticos vinham quase sempre associados a suas representações gráficas bidimensionais ou mesmo tridimensionais.

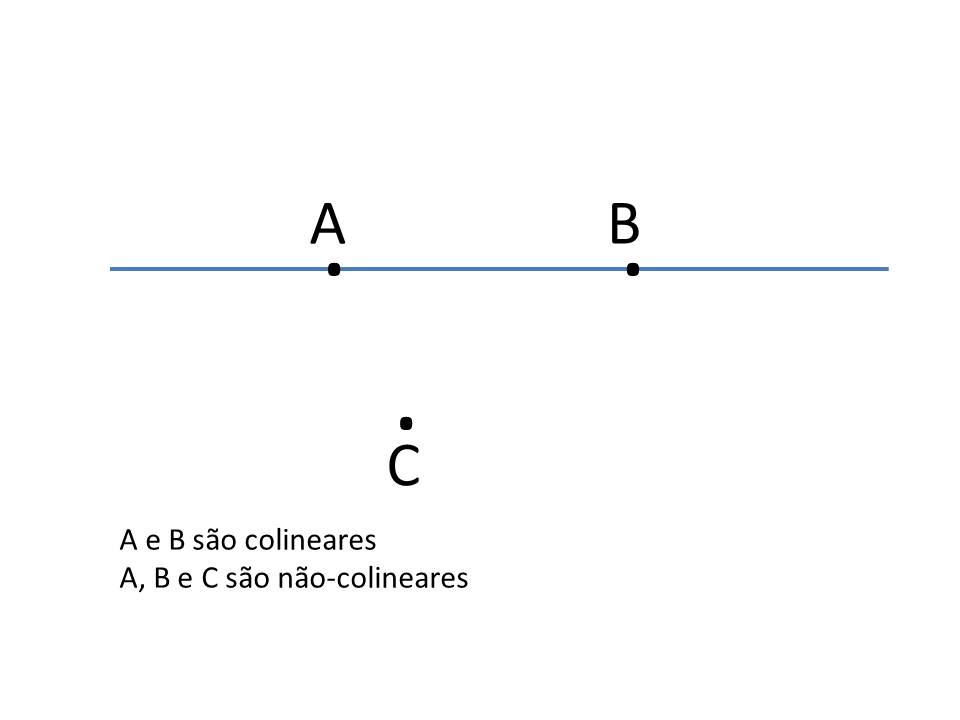
Como escrito acima, o postulado tema desse texto não foi enunciado por Euclides. Apesar disso, é um conhecimento consequente de seus trabalhos e parte essencial da geometria clássica como a estudamos até hoje. Talvez não seja possível descobrirmos quem primeiro enunciou a frase dessa forma, mas isso pouco importa.

Voltando à mesa bamba

As figuras A e B abaixo nos auxiliarão no entendimento da instabilidade da mesa bamba. O problema da nossa mesa é que um de seus pés representará sempre um ponto fora do plano definido pelos pontos A, B e C, ou seja, há um ponto de apoio restante (a extremidade da perna mais curta, sem contato com o solo, representada pelo ponto D), acima do plano “β” (figura A).

Quando apoiamos os cotovelos na região do tampo da mesa sobre a perna mais curta, fazemos com que ele se mova. O movimento, que será tanto maior quanto mais curta a perna, representa um desequilíbrio da mesa. Um equilíbrio momentâneo será alcançado quando a perna mais curta tocar o solo, ou seja, um novo apoio determinado por três pontos (A, C e D) no plano “β” (figura B).

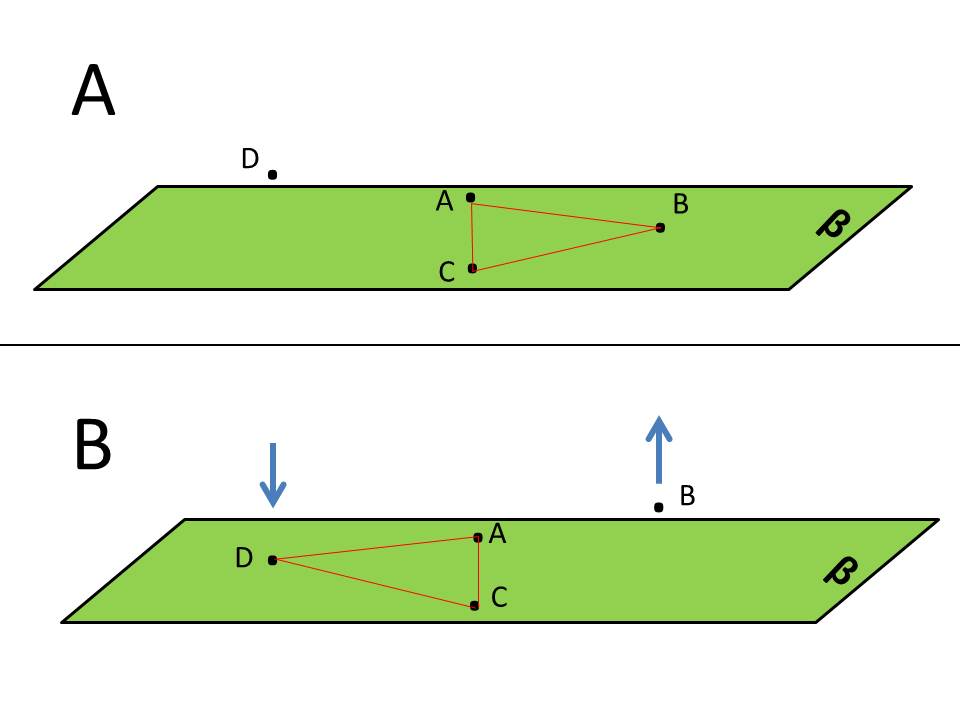
Acontece que a mesa nunca conseguirá apoiar quatro pontos ao mesmo tempo (o que geraria um equilíbrio estável) porque os quatro pontos não estão no mesmo plano (não coplanares).

Como podemos notar, a diferença de tamanho nas pernas da mesa nesse exemplo acontece com pernas opostas, ou seja, em uma diagonal. A situação seria ainda pior se duas pernas opostas fossem menores que as outras duas.

Há mesas muito charmosas mundo afora, nas quais todos teríamos a noção de aconchego, porque se parecem com as das casas de nossas avós ou porque agora o rústico está na moda. A foto abaixo mostra uma cadeira de quatro pernas. Note que a mesa tem três pernas (apoiadas ao mesmo tempo, claro), enquanto a cadeira tem três apoiadas e uma suspensa, pronta a dar um susto em quem nela se sentar.

Euclides de Alexandria

Se eu convidasse o Euclides de Alexandria para tomar um café pela primeira vez (não há indício de que os gregos do período conhecessem café), mostraria que sou um bom aluno escolhendo uma mesa de três pernas. Como já sabemos, qualquer que seja o solo, uma mesa de três pernas será estável, pois terá apenas um plano de apoio. Claro que podemos argumentar que o chão pode ser tão irregular ou uma perna tão curta que a mesa de três pernas e seu conteúdo caiam. Mesmo assim, só haverá um plano de apoio.

Muito pouco é sabido sobre a vida de Euclides, por isso, permiti a mim mesmo imaginar que tomaríamos um café. Muito do que escreveu parece estar perdido para sempre. Sua obra mais completa a chegar até nós é “Os elementos”, um livro sobre geometria plana e espacial, mas também sobre teoria dos números e algum conhecimento sobre outras áreas correlatas. Historiadores da matemática a consideram o texto mais influente da civilização ocidental depois da Bíblia Sagrada.

É consenso que nem tudo que aparece nos textos de Euclides é originário seu, fato comum na Antiguidade. Lembremos que grandes gênios da humanidade, como Platão e Aristóteles, fizeram parte de seus trabalhos na forma de grandes e importantes sínteses do conhecimento anterior, negando-o ou reforçando-o, realizando ajustes e correções, e, muitas vezes, acrescentando conhecimento totalmente novo. Esse parece ter sido o caso de Euclides.

Acredito que Euclides também se preocuparia com a questão da quantidade de massa e onde esta seria colocada no tampo da mesa de três pernas, o que, se mal distribuído, poderia fazê-la tombar. Mas, com relação ao nosso problema inicial, sem dúvida, uma mesa de três pernas é mais estável que uma de quatro na maioria das vezes, mesmo em um terreno irregular. Não importa o quão irregular é o chão, três pontos não colineares sempre estarão em um e somente um plano de apoio.

Planos e suas aplicações no dia a dia

Não apenas quem constrói cadeiras e mesas deve estar atento à definição de plano, pois muitas outras atividades do dia a dia demandam essa noção.

Em computação gráfica, por exemplo, ao definir um plano de corte de uma figura tridimensional, se deve escolher três (e somente três) pontos para, em seguida, um software realizar o corte da figura através daquele plano.

O plano cartesiano (em homenagem a seu idealizador, René Descartes), um plano dividido em quatro quadrantes por duas retas perpendiculares entre si, permitiu o surgimento da geometria analítica e com ela uma infinidade de aplicações em áreas como engenharia, física, design, astronomia etc. O sistema GPS de geolocalização utiliza esse sistema cartesiano em vários planos especiais da Terra, dentre eles o que passa pela linha do Equador e o que passa pelo meridiano de Greenwich.

Na primeira aula de anatomia humana são apresentadas formas de referência espacial para padronizar a localização das estruturas (órgãos e sistemas). Uma dessas formas é a divisão do corpo humano através de planos. A figura abaixo mostra os três principais planos de divisão e orientação espacial para o corpo humano.

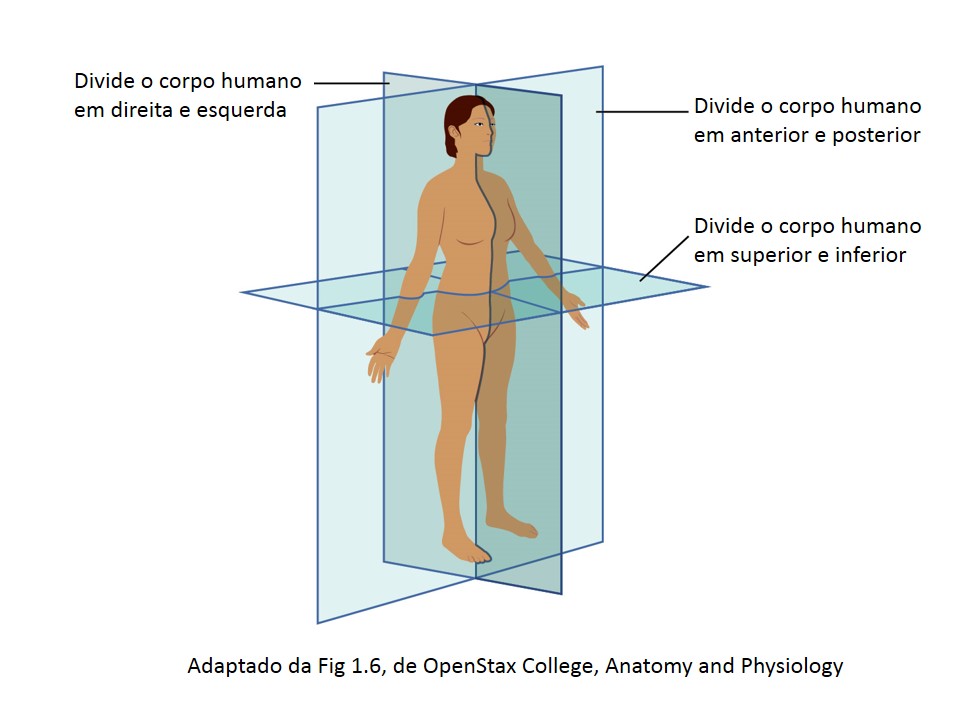
Há muitas outras situações nas quais assegurarmos que uma superfície é plana e estável tem importância. É só olhar ao redor. Alguns conhecimentos, de tão presentes em nossas vidas, passam despercebidos. A matemática tem muito disso, está presente em tudo. Ou, como Pitágoras parece ter dito (já que não há fonte confiável de um texto seu): “há números em tudo” ou “tudo é feito a partir de números”, mas o significado dos dizeres dos filósofos pitagóricos fica para outro texto…

Uma pergunta final: há alguém que tenha contribuído para o conhecimento científico (pode já ter morrido) com quem você gostaria de tomar um café? Já havia pensado nisso? Além do Euclides, tenho muitos outros.

* Tradução por Irineu Bicudo

Para saber mais sobre o tema:

– EUCLIDES. Os elementos. São Paulo: Editora UNESP, 2009. (traduzido do grego por Irineu Bicudo)

– EVES, H. Introdução à história da matemática. Campinas: Editora Unicamp, 2004.

– BOYER, C. C. História da matemática. 3ª Edição. São Paulo: Blucher, 2012.